Nota: questa risposta è stata migrata da physics.SE, quindi ho dovuto rieseguire il rendering delle formule come immagini. La risposta è specifica anche per l'apprendimento della fisica, sebbene potrebbe funzionare anche per altri campi.

Questo sembra un classico problema XY. Non conosco nessun fisico praticante che usi uno speciale schema di memorizzazione "senza capire", e penso che una cosa del genere sarebbe controproducente. Ecco alcuni suggerimenti che potrebbero invece essere utili.

1. Usa le maniglie concettuali

Ecco le formule per la velocità del suono in un gas, la velocità delle onde su una corda e le frequenze di oscillazione di una massa su una molla e un pendolo fisico.

L'intuizione per tutti loro è la stessa: il numeratore è una certa misura di una forza di ripristino, indipendentemente dalla forza del gas spinge indietro, la forza con cui tira la corda, la forza della molla o la coppia di gravità. Il denominatore è sempre una misura di inerzia, proporzionale alla massa del sistema. Grazie a questa intuizione non devo ricordare nulla, tranne che si tratta di una radice quadrata.

Come altro esempio, considera tutte le fastidiose conversioni tra quantità d'onda,

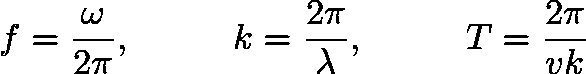
insieme a molti altri. Per ricordare le conversioni tra (ω, k) e (T, λ), uso semplicemente

che è la definizione fondamentale di il quadrivettore numero d'onda. Questo risolve i fattori di 2π, poiché è il cambiamento di fase di un ciclo. Non c'è posto dove tutti questi piccoli trucchi siano scritti; ognuno ha il proprio ed è meglio se lo fai tu stesso mentre procedi.

2. Non preoccuparti del giudizio

Stavo solo guardando una lezione della scuola estiva in cui un rinomato fisico teorico ha impiegato 30 secondi buoni per capovolgere una frazione. Questo è del tutto tipico e per niente imbarazzante. Alcune persone funzionano meglio riorganizzando i simboli nella loro testa e alcune funzionano meglio usando il gesso o la carta. Personalmente non posso fare niente nella mia testa; Devo usare la carta o scriverlo per aria, ma non mi sono mai sentito giudicato per questo. Se i tuoi colleghi sono in grado di giudicare, sono scortesi e non dovresti lasciarti abbattere.

Quando vedo qualcuno in grado di ricordare o riscrivere qualcosa molto più velocemente di me, spesso gli chiedo quale sia il suo le maniglie concettuali sono. A meno che la persona non sia eccezionalmente scortese, in genere è felice di spiegare. (Questo è particolarmente vero in fisica, dove la semplice memorizzazione non è cool.)

3. Concetti di blocchi, separatamente dagli strumenti

Se hai problemi a scrivere una proposta di sovvenzione, la soluzione non è memorizzare l'esatta sequenza di attivazioni muscolari necessarie per scrivere ogni singola lettera. Allo stesso modo, se la fisica sembra troppo "grande", la cosa peggiore che puoi fare è renderla ancora più grande, scompattando ogni equazione in otto equazioni separate. L'apprendimento avviene invece raggruppando le cose insieme.

Ad esempio, prendi la derivazione dell'equazione delle onde, che è composta da due pagine complete di matematica. Non vuoi memorizzare ogni riga nella tua testa. Invece, vuoi solo memorizzare un'intuizione generale che "curvatura significa una forza di ripristino perché le corde sotto tensione si raddrizzano", che ti dà il termine ∂²y / ∂x². Per arrivare al risultato finale è necessario conoscere la seconda legge di Newton (dando il termine ∂²y / ∂t²), l'approssimazione del piccolo angolo e l'approssimazione binomiale. Ma nessuno di questi è specifico per l'equazione delle onde: sono solo strumenti generali.

Come altro esempio, mi sono perso quando sono stato esposto per la prima volta alla notazione tensoriale. Sembrava che ci fosse un'enorme quantità di cose da memorizzare! Ma è svanito una volta che mi sono seduto e ho scritto tutte le manipolazioni consentite. Si scopre che non ce ne sono molti, al massimo dieci comuni. Tutti i calcoli tensoriali fino al livello universitario utilizzano gli stessi dieci passaggi più e più volte, quindi in senso tecnico è in realtà più facile dell'algebra delle scuole superiori, che ha molte più manipolazioni consentite. Una volta che hai questa comprensione, molte derivazioni diventano più brevi; vengono suddivisi in "usa i passaggi standard, più questo trucco nel mezzo".

Quindi tutto ciò che devi fare è ricordare il trucco, idealmente con una maniglia concettuale.

4. Costruisci la tua comprensione

Come ho sottolineato sopra, il modo migliore per ottenere questo tipo di comprensione è costruirla tu stesso! Non c'è da vergognarsi nel rivisitare un argomento che è "di base" e ricostruirlo da soli da zero; L'ho fatto con il calcolo e la meccanica diverse volte ogni volta che mi sentivo arrugginito. Crea un foglio delle formule o, se pensi visivamente, prova a disegnare una mappa mentale o un diagramma delle dipendenze. Sfida te stesso a rieseguire le equazioni chiave senza un riferimento. Se lo fai spesso, costruirai naturalmente le necessarie maniglie e blocchi concettuali e migliorerai nel riconoscere quale strumento usare.

Mi piace molto la risposta di @ knzhou, che penso faccia un ottimo lavoro nell'affrontare il problema in modo più o meno canonico. Per aggiungere a ciò, parte della tua falsa premessa (ciò che @knzhou chiama il tuo problema XY) è che stai cercando di compartimentalizzare "memoria" e "comprensione" come due cose separate e indipendenti. Non è così che funziona il cervello. In pratica, ricordare e capire le cose sono due aspetti dello stesso insieme di fenomeni mentali. Quando si comprende correttamente la derivazione di una formula, non è solo che si è in grado di ricostruire la derivazione e la formula su richiesta dati tempo e carta e penna, ma diventa anche molto più facile ricordare la formula senza la derivazione. Ciò è dovuto alle maniglie concettuali (per usare la terminologia molto appropriata di @ knzhou) che sviluppi attraverso il processo di acquisizione di quella buona comprensione.

In effetti, penso che sia possibile memorizzare facilmente o meno una formula in molti casi può essere utilizzato come un buon segnale per verificare se si è acquisita la necessaria comprensione della derivazione / ragionamento che sta dietro ad essa. Se trovi ancora la formula poco intuitiva e difficile da ricordare, o generalmente ti senti a disagio con ciò che dice la formula, è possibile che tu non abbia interiorizzato la logica dietro di essa (forse perché ti stai concentrando troppo sulla memorizzazione la derivazione stessa piuttosto che pensare e capire davvero perché ogni passaggio è naturale e come le diverse parti si incastrano). Gli esercizi mentali suggeriti da @knzhou possono essere un buon modo per portarti a quel livello, che è un livello di comprensione più elevato rispetto alla semplice lettura di una dimostrazione o derivazione e alla verifica che sia corretta.

Inoltre a questo, il consiglio di @ knzhou di preoccuparsi di meno della tua capacità di elaborare formule al volo quando altre persone stanno guardando sembra anche molto sensato.

Per me (un matematico), il processo si basa sulla ripetizione delle formule abbastanza spesso. Ad un certo punto comincio a indovinare quale potrebbe essere la risposta giusta, quindi farò il calcolo (mentale o cartaceo) per verificare. Qualche ripetizione in più, e non avrò più bisogno di verificare.

Per alcune formule ci sono trucchi specifici, che di solito riguardano test con casi speciali molto semplici e controllando che il risultato abbia senso. Ad esempio, sin ( θ ) = x o sin ( θ ) = y , ma qual è stato ? Ricordo che sin (0) = 0 e ricordo dove punta l'angolo zero nel cerchio unitario, il che mi consente di dedurre quale alternativa è corretta. (Vera soluzione lasciata come esercizio.)

In fisica, ho bisogno di ricordare se devo dividere o moltiplicare per una certa quantità. Oltre a controllare le unità, potrei lasciare che la quantità vada a zero o all'infinito e considerare cosa dovrebbe accadere allora. v = s / t o v = t / s ; se la distanza rimane costante ma il tempo va all'infinito, la velocità deve essere piccola, il che mi permette di scegliere l'alternativa giusta. (In realtà lo controllo guardando le unità, ma l'esempio dovrebbe illustrare la tecnica.)

Il metodo che ho sempre trovato più efficace è quello di creare una parola o un inizialismo dalle lettere nella formula , inserendo vocali / consonanti secondo necessità.

Esempi:

1. Per ricordare la formula del dominio di Laplace per il primo elemento di ritardo dell'ordine PT1 nell'ingegneria di controllo

   

   nota che il denominatore pronuncia "1 °"!

2. Per ricordare la formula per l'invarianza temporale

   

   Ho trattato il delta maiuscolo come una "A" e ho ricordato "futa" (parola giapponese per "ermafrodita") che ovviamente ha senso solo se hai familiarità con la parola.

3. Allo stesso modo, uso "Uli" (nome tedesco) e "ICU" (unità di terapia intensiva) per ricordare questa coppia di formule in elettronica, immaginando il mio amico in terapia intensiva:

   

   

Uso un'idea simile anche per ricordare elenchi (usa le loro prime lettere, ad esempio PAGINA per ricordare che gli agenti razionali hanno p ercezioni, a st rong> ctions g oals and an e nvironment) e definizioni (trova un mnemonico nel suo nome, ad esempio, in bioinformatica, B LAST estende una corrispondenza in b altre direzioni mentre F AST calcola o FF serie).

Per quanto ne so non esiste un sistema di memorizzazione classico e consolidato per le formule. La maggior parte delle persone nelle arti della memoria si è concentrata sulla memorizzazione di numeri o testo (o carte).

Tuttavia, ci sono stati alcuni schizzi di come può essere fatto nella comunità delle arti della memoria. Questo thread discute vari suggerimenti, inclusa la definizione di immagini per i simboli (il segno integrale è un violino), i sistemi di pioli per gli elenchi o l'utilizzo del metodo dei loci per aggirare la formula. Idee simili possono essere trovate qui.

Questo metodo presuppone che tu conosca altre arti della memoria di base. Questo è ovviamente il problema, ci vuole un bel po 'di allenamento prima di essere bravo con loro. Ho conseguito il dottorato di ricerca sulla memoria, ho lavorato per anni sul miglioramento umano e spesso ho bisogno di ricordare varie formule ... eppure non uso le arti della memoria per loro. Un misto di pigrizia e costo alternativo me ne ha impedito; il compromesso può essere diverso per gli altri.

Generalmente quando memorizzo le formule cerco di familiarizzarmi con loro - impara a conoscere ogni fattore, termine e simbolo e perché sono presenti. Una volta che hai una rete di collegamenti puoi ricostruire la formula abbastanza facilmente a meno che non sia qualcosa di arbitrario e senza struttura come

• 4.652 x ⁴ + 0.4587843 x ³ - 0.434343 x + 17.

Ma se hai bisogno di snocciolare tali formule ancora e ancora potresti voler riconsiderare quello che stai facendo.

Infine, creare e avere un cheat sheet di formule usate spesso non è nulla di cui vergognarsi. È utile. Recentemente ho creato un file standard da includere con costanti fisiche e formule nel mio codice, e ha reso il mio progetto attuale (un libro che ne scrive uno) notevolmente più facile e meno frustrante. Non c'è niente di sbagliato nell'esternalizzare la tua mente al Libro di gomma se riesci a cercare le cose abbastanza velocemente.

Per le permutazioni delle formule, è meglio acquisire maggiore familiarità con l'algebra e apportare le trasformazioni necessarie sul posto.